- Rebar Table
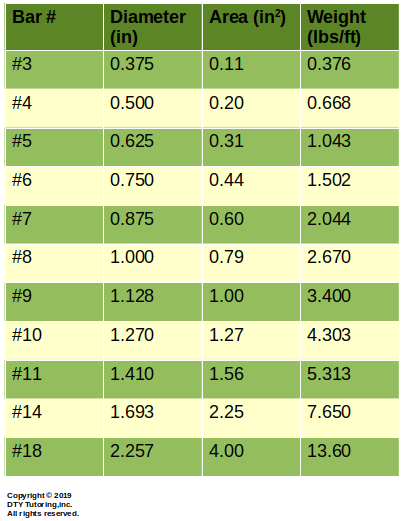Figure 1: Rebar Information Table (ASTM)
- Relationship between Shear (V) and Moment (M) diagrams and steel reinforcements in a simply supported and cantilever beam.
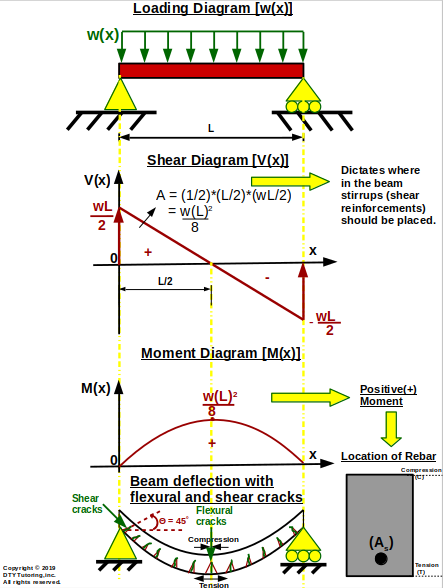
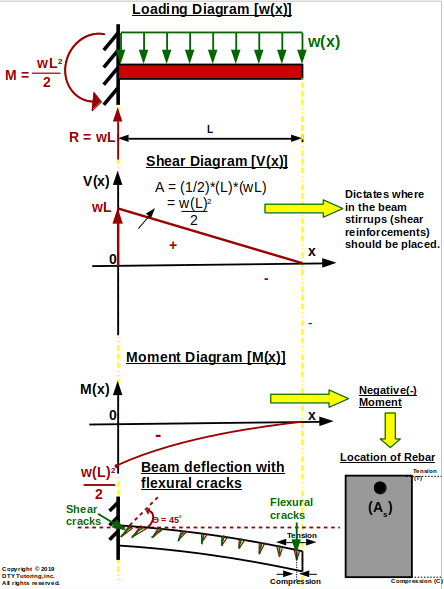Figure 2: Relationship between Shear (V) and Moment (M) diagrams and steel reinforcements in a simply supported and cantilever beam
- Meaning of singly and doubly reinforced beams
Tension reinforced section is when you have steel reinforcement (rebar) on the tension controlled region where the rebar is used to counteract the lack of tensile strength in concrete. When reinforcement is only present in the tension zone, you have a singly reinforced beam. Nevertheless, sometimes, rebar on the tension side only is not enough to resist the ultimate moment capacity of the beam, therefore, reinforcement in the compression region is needed. When reinforcement is present in both zones (tension and compression), you have a doubly reinforced beam.
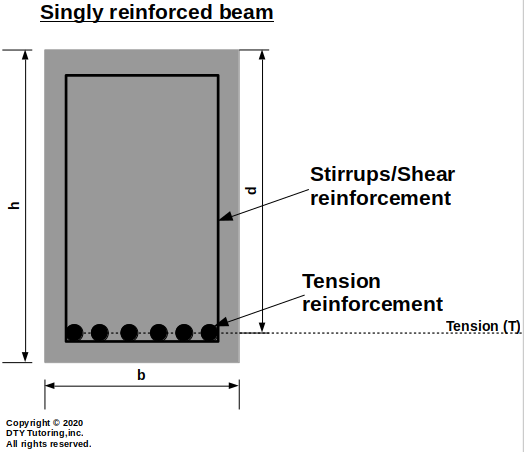
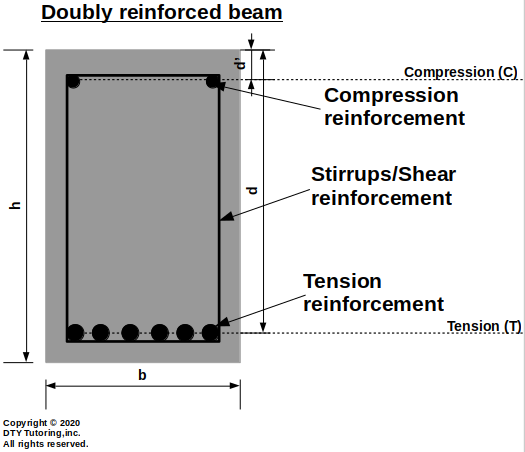Figure 3:Singly and doubly reinforced beam explanation
Worked out problems with solutions in pdf files
Cracks in an Unreinforced Beam
Draw the cracks in an unreinforced concrete simply supported beam subjected to a uniform distributed load acting downwards. (transverse and longitudinal)
Figure 4: Simply Supported Beam with Uniform Distributed Loading (UDL)
Ultimate Moment Capacity for a Singly Reinforced Beam
Find the ultimate moment capacity (Φ Mn) for the singly reinforced rectangular beam shown below.
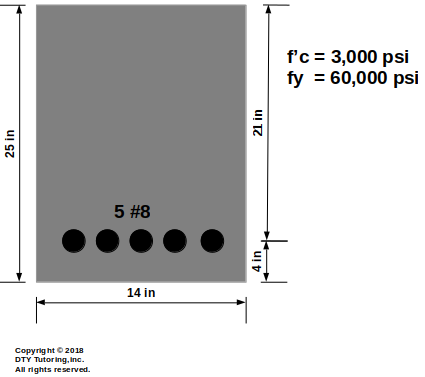Figure 5: Singly reinforced concrete beam analysis example 1 (Beam)
Find the ultimate moment capacity (Φ Mn) for the singly reinforced rectangular beam shown below.
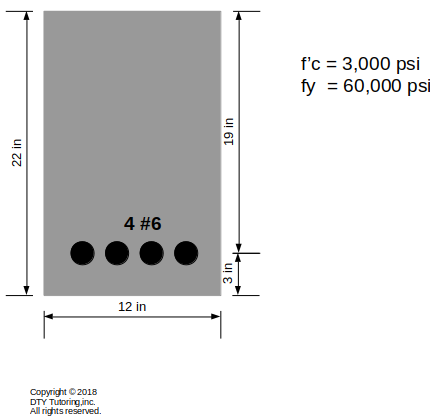Figure 4: Singly reinforced concrete beam analysis example 2 (Beam)
Find the required height, h, of the reinforced concrete cross section for the simply supported beam with a uniform live and dead load (self-weight included) as shown below, assuming that the steel has yielded (use factored loads).
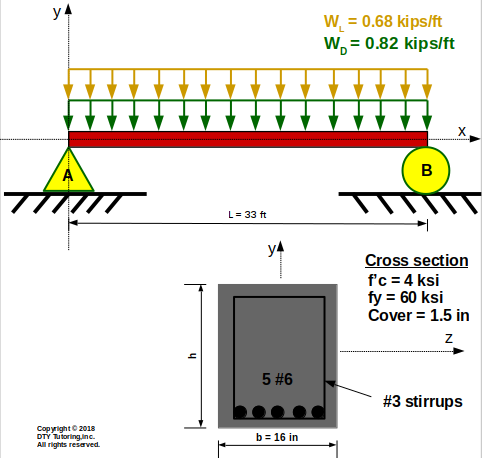Figure 5: Simply supported beam with a singly reinforced concrete cross section
Find the uniformly distributed live load, wL, of the reinforced concrete cross section for the simply supported beam with a uniform live and dead load (self-weight is not included) as shown below, assuming that the steel has yielded (use factored loads).
The unit weight of the reinforced concrete section, ϒconc is 150 pcf.
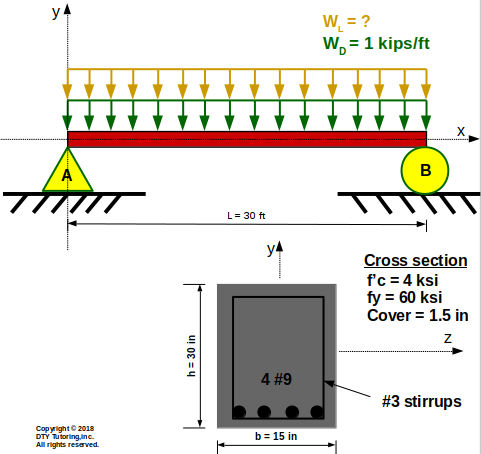Figure 6: Simply supported beam with a singly reinforced concrete cross section
Ultimate Load for a Column
Find the ultimate load (ΦPn) for the short tied column as shown below.
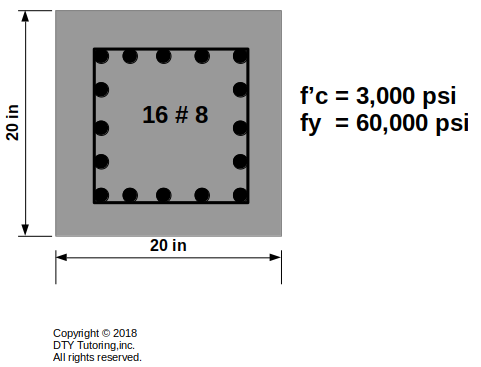Figure 7: Short tied reinforced concrete column example
Under-reinforced or Over-reinforced
For the singly reinforced concrete beam as shown below, check if beam is under-reinforced or over-reinforced.
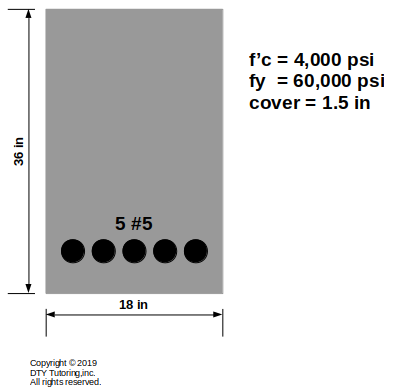Figure 8: Singly reinforced concrete beam
Ultimate Moment Capacity for a Doubly Reinforced Beam
Find the ultimate moment capacity (Φ Mn) for the doubly reinforced concrete rectangular beam shown below.
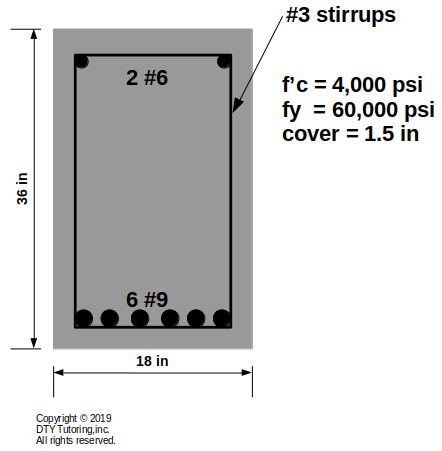Figure 9: Doubly Reinforced Beam Analysis Ex1 (Beam)
Ultimate Moment Capacity for a T-beam With Two Rows of Steel in Tension
Find the ultimate moment capacity (Φ Mn) for the reinforced concrete T beam with 2 rows of steel as shown below.
.png)
Figure 10: Reinforced T Beam Analysis with 2 rows of steel (Ex1)
Ultimate Moment Capacity for a singly reinforced L-beam
Find the ultimate moment capacity (Φ Mn) for the singly reinforced L-beam .
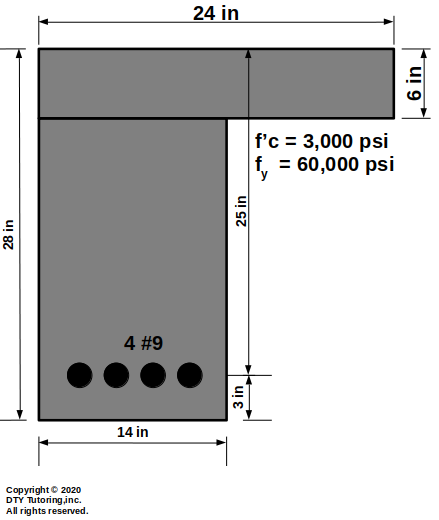Figure 11: Singly Reinforced L-beam
Ultimate Moment Capacity for a Singly Reinforced Trapezoid beam
Find the ultimate moment capacity (Φ Mn) for the singly reinforced concrete trapezoid beam as shown below.
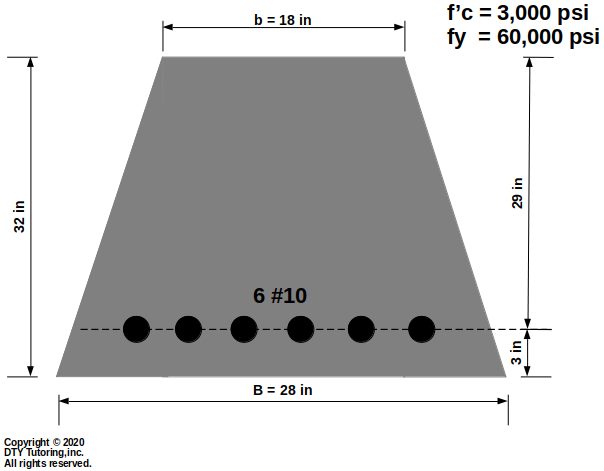Figure 12: Singly Reinforced Concrete Trapezoid Beam
Shear Reinforcement Analysis and Design
Find the ultimate shear capacity (Φ Vn) for the singly reinforced rectangular beam shown below.
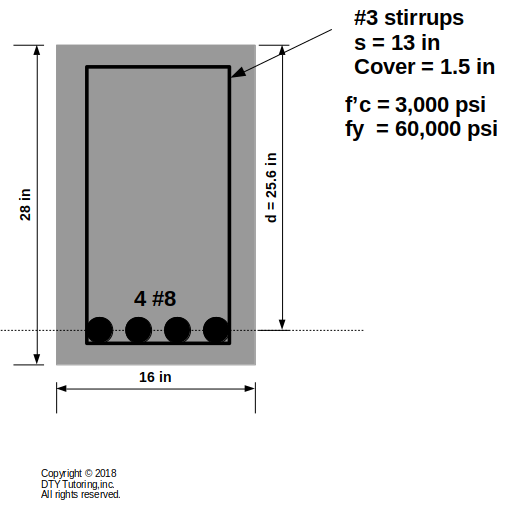Figure 13: Singly reinforced concrete beam analysis example 3 (Beam)
Design the shear reinforcement (stirrups) for this 24 ft span simply supported reinforced concrete beam as shown below. Self-weight of the beam is not included in the dead load, ϒconc = 150 pcf.
(a)Find Vu @ d,
(b)Find the ultimate shear strength provided by concrete (Φ Vc) from cross section,
(c)Find (Φ Vc)/2 from cross section,
(d)Are stirrups required?
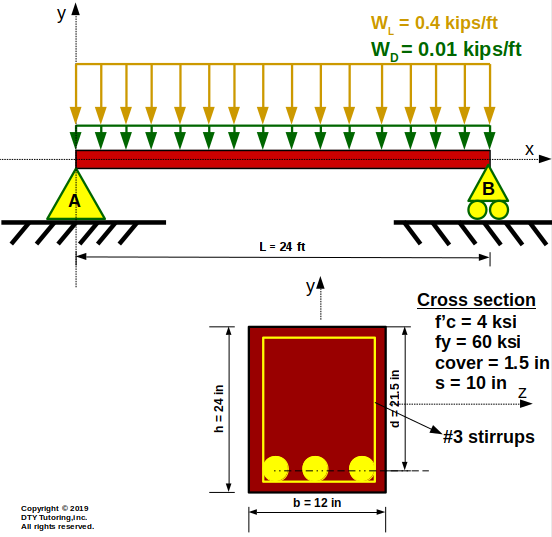Figure 14: Simply supported reinforced concrete beam (shear reinforcement problem)
Design the shear reinforcement (stirrups) for this 28 ft span simply supported reinforced concrete beam as shown below. Self-weight of the beam is not included in the dead load, ϒconc = 150 pcf.Sketch the stirrups pattern.
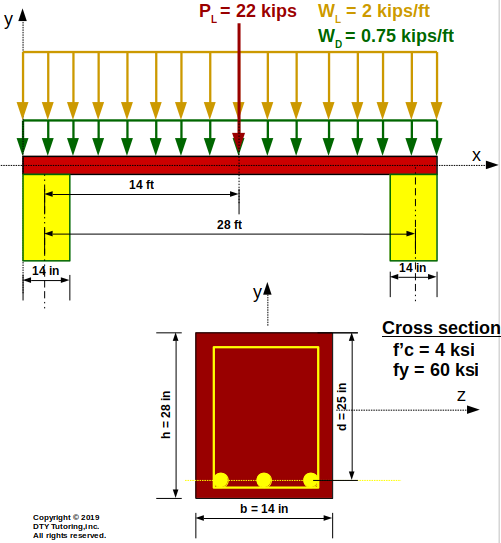Figure 15: Simply supported reinforced concrete beam (shear reinforcement design problem)
Reinforced Concrete Beam Design (Flexural and Shear)
Design this 28 ft span cantilever beam as shown below, using #3 stirrups. Self-weight of the beam is not included in the dead load, ϒconc = 150 pcf.
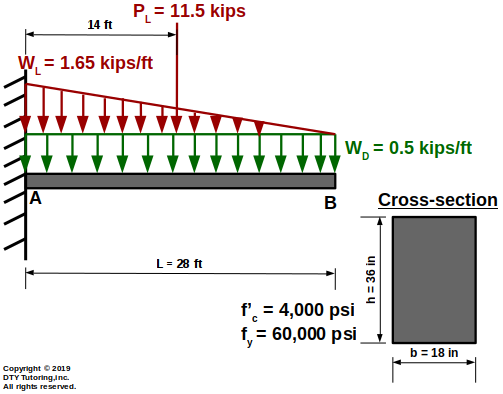Figure 16: Cantilever beam reinforced concrete design
-
-
